Что такое транспортир? Правила измерения углов
Измеритель углов — транспортир KWB

Строительный измеритель углов или транспортир KWB класса DIY. Какая у него точность измерения, как с ним работать и нужен ли он вообще? Разбираемся вместе.
Основные характеристики
| Тип: | транспортир |
| Из чего сделан: | пластик |
| Диапазон измерения углов: | от 0° до 180° |
| Цена деления основной шкалы: | 1° |
| Точность измерения: | до 10′ (одна шестая градуса) |
| Артикул: | 065800 |
Транспортир KWB по всем признакам относится к измерительным приборам уровня домашнего мастера. Пластик, шкалы, нанесенные краской. Доступная цена. Проживание на полках строительных гипермаркетов. Конкретно этот был приобретен в Кастораме.

Но что уж точно не отнять у транспортира, так это необычность конструкции и качество сборки. В нём четыре оси вращения, и ни в одной не наблюдается люфта. Планки вращаются довольно туго. Имеется фиксирующее колесо. Выставленный по измеряемому углу транспортир можно уронить (не со второго этажа конечно) — он сохранит зафиксированный угол.

Шкалы транпортира
Транспортир KWB имеет две шкалы — основную и вспомогательную.
Шкалы хоть и нанесены краской, но считываются однозначно. Правда стойкость к износу у них ограничена.

У основной шкалы четыре ряда значений. Один нанесен сверху шкалы, три снизу — видны в смотровое окошко подвижной планки. Каждый ряд используется для своего метода измерения углов. Каждый метод опишем подробно ниже.
Цена делений основной шкалы — один градус.
Вспомогательная шкала на подвижной планке размечена под измерение долей градуса. Цена делений — 10′ (десять минут). То есть можно измерять углы с точностью до десяти минут или до 1/6 градуса (в десятичной системе).
Измерение углов
Как измерять углы транспортиром? Покажем наглядно на иллюстрациях.
Метод 1

При этом методе размер угла определяется с помощью внешней шкалы. Предельный угол, который можно измерить таким методом, равняется 110 градусам.
Метод 2

Второй метод применим для измерения тупых углов от 90° до 180°.
Для измерения используется вторая внутренняя шкала.
Метод 3

Третий метод также работает в диапазоне измерений от 15° до 180°.
Размер угла определяется по второй внутренней шкале.
Метод 4

Четвертый метод — это модификация третьего. Доступный диапазон измерений от 0° до 75°.
Размер угла определяется по третьей внутренней шкале.
Метод 5

Пятый метод представляет собой модифицированный метод №2 только для острых углов от 15° до 90°.
В этом методе используется вторая внутренняя шкала.
Метод 6

Шестой метод позволяет измерять углы от 90° до 165°.
При этом методе используется первая внутренняя размерная шкала.
Измерение углов транспортиром на практике
Измерим угол загиба монтажной лопатки на гвоздодёре Sparta 300 мм . Метод замера №2. Угол = 21°.

И угол загиба самой гвоздодёрной части. Метод замера №2. Угол = 153°40′.

А какой угол заточки у топора Outventure 44х12 см ? Метод замера №1. Ответ — угол = 30°.

Посмотрим, какой угол скоса у пассатиж в мультитуле Leatherman Sceletool Coyote. Метод замера №4. Угол = 30°60′.

И насколько широк угол размаха челюстей в ручных тисках Jonnesway . Метод замера №5. Угол = 34°.

И напоследок угол заточки режущих кромок у бокорезов Jonnesway P1017 . Метод замера №1. Угол = 70°.

В сетевых магазинах транспортир предлагается по цене около 250 рублей (или $3.5).
Заключение
Транспортир KWB или как указывают в ценники продавцы «измеритель углов» показал себя удобным и полезным девайсом. С ним не придётся ломать голову, как замерить хитрые угловые размеры заточки режуще-рубящих кромок. И для проверки правильности углов при строительстве ему тоже найдётся применение.
Что такое транспортир? Правила измерения углов
Транспортир является самым распространенным инструментом, для того чтобы измерить величину углов. Термин «транспортир», что в переводе с французского обозначает «переносить».

Этот инструмент может иметь разный внешний вид, но у любого транспортира есть шкала, которая расположена на полуокружности. Центр этой шкалы отмечен штрихом или отверстием.
А теперь давайте рассмотрим этот полукруглый предмет и найдем отверстие в центре его плоского угла. Отверстие в транспортире является точкой отсчета и с этой точки начинается линия начала отсчета, которая проходит вдоль всей плоской части транспортира.
Транспортир относится к довольно простому ручному инструменту, с помощью которого можно рисовать и измерять любые углы. Научившись им пользоваться, у вас не будет проблем в решении задач, связанных с измерением углов.
Измерение углов
Измерение углов происходит путем сравнения угла измеряемого с углом, который служит единицей измерения. Для этого нужно внутреннюю часть измеряемого угла постепенно заполнить единичными углами, плотно укладывая один к другому. Количество уложенных углов дает меру угла измеряемого. Самым удобным и распространённым инструментом для измерения углов является транспортир.
В качестве единицы измерения угла может выступать любой угол или другая общепринятая единица измерения.
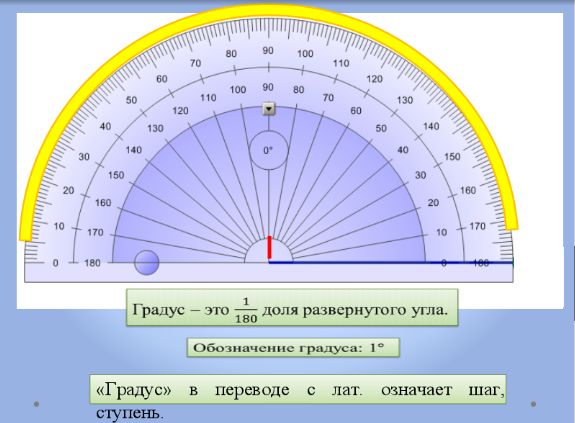
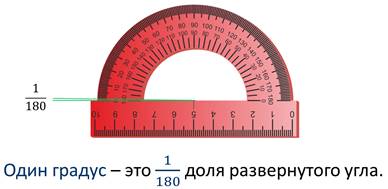
Такой единицей может быть один градус, который составляет 1/180 часть развернутого угла. Поэтому в развернутый угол можно уложить сто восемьдесят углов, равных одному градусу.
Для более наглядного примера берем модель половинки пирога или пиццы, которые разрезаны на сто восемьдесят равных кусочков и плотно уложены один к другому. При этом мы видим, что стороны углов совмещаются со стороной развернутого угла, а дойдя до последней, мы увидим, что она совпадет с другой стороной развернутого угла.
Так на примере картинки в низу, мы видим, что в одну шестую развернутого угла, угол в один градус можно уложить тридцать раз, а в половину развернутого угла – 90 раз.
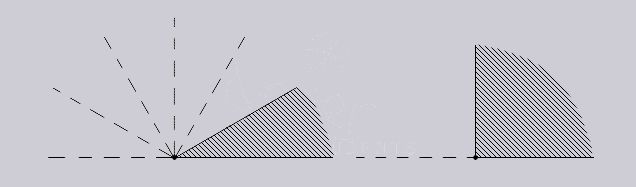
Если же необходимо измерить угол, который менее одного градуса, то в таких случаях используют другие единицы измерения, например минуты или секунды.
Градусной мерой угла называют положительное число, которое нам показывает то количество раз, которое градус или его части уложились в данном угле.
Но теперь вы уже узнали, что для измерения углов, чаще всего используют такую распространенную единицу измерения, как градус. Его угол равен одной сто восьмидесятой части развернутого угла.
Для удобства измерения углов используют такой чертежный инструмент, как транспортир.
Как измерить угол с помощью транспортира
А сейчас приступим к измерению угла при помощи такого инструмента, как транспортир. Чтобы измерить угол с помощью транспортира, необходимо выполнить несложные действия. Для этого нужно:
• Во-первых, отметить на вершине угла, который вы будете измерять, начальную точку отсчета.
• Во-вторых, нужно совместить нижнюю линию угла с линией, с которой будет осуществляться начало отсчета.
• Далее необходимо отметить на бумаге расположенные цифры, которые бы соответствовали измеряемому углу.
• Следующим вашим шагом будет проведение линии, которая пересекает разметку транспортира. Цифра же, расположенная на месте этого пересечения, указывает на угол в градусах.
• Так как на некоторых транспортирах имеются две противоположно направленные шкалы, то это позволяет измерять углы, которые направлены в разные стороны.

Задание
На рисунке вам предоставлены разные виды углов.
1. Какие углы изображены на картинке? Назовите их.
2. С помощью транспортира измерьте приведенные на рисунке углы и запишите их значение:
презентация по теме «Транспортир», история и правила пользования

данная работа рассказывает об истории появления и развития транспортира, о его разновидностях и правилах пользования
Скачать:
| Вложение | Размер |
|---|---|
| transportir.pptx_1.pptx | 1.59 МБ |
Предварительный просмотр:
Подписи к слайдам:
Транспортир Автор: Валерия Терентьева 7 “ Г ” класс ГБОУ СОШ №1220 г. Москва . .
Н.Е. Жуковский В математике есть своя красота, как в живописи и поэзии.
Что такое транспортир? Транспорти́р — инструмент для построения и измерения углов. Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0 до 180°. В некоторых моделях — от 0 до 360°. .
Из чего делают транспортиры? Транспортиры изготавливаются из стали,пластмассы,дерева и других материалов. .
История транспортира История не сохранила имя ученого, который изобрел транспортир – возможно в древности этот инструмент имел совсем другое название. Современное название происходит от французского слова ”ТRANSPORTER”, что означает “переносить”. Предположительно, транспортир изобрели в древнем Вавилоне. .
Разновидности транспортиров Полукруговые (180 градусов) — наиболее простые и древние транспортиры. Круговые (360 градусов). Геодезические, которые бывают двух типов: ТГ-А — для построения и измерения углов на планах и картах; ТГ-Б — для нанесения точек на чертежной основе по известным углам и расстояниям. Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр. Улучшенные типы транспортиров, которые необходимы для более точных построений и измерений. Например, существуют специальные транспортиры с прозрачной линейкой с угломерным нониусом, которая вращается вокруг центра. .
Для чего нужен транспортир? Транспортир — инструмент, широко используемый в геометрии. При этом обойтись без этого инструмента достаточно трудно как школьникам, решающим свои первые задачи, так и инженерам, выполняющим сложные геометрические построения. Чаще всего транспортир используется для получения градусной меры угла.Без транспортира мы не сможем измерить угол. .
Как пользоваться транспортиром? Для измерения угла необходимо поместить его вершину в точку начала отсчета, обозначенную на линейке транспортира. Затем необходимо обратить внимание на то, чтобы сторона угла, направленная на угломерную шкалу, пересекала ее. В случае, если длина этой стороны оказывается недостаточной, следует продлить ее до пересечения угломерной шкалы. После этого нужно посмотреть, на каком значении сторона угла пересекает указанную шкалу. В случае, если измерению подвергается острый угол, искомое значение будет меньше 90°, а при измерении тупого угла следует пользоваться той частью шкалы, которая содержит деления, превышающие 90°. Аналогичным образом осуществляется построение углов при помощи транспортира. Сначала следует провести линию, которая будет представлять собой одну из сторон, а ее окончание, которое станет вершиной, поместить в точку отсчета. Затем на угломерной шкале точкой нужно отметить нужную величину угла, который может быть как острым, так и тупым. После этого, убрав транспортир, соедините вершину будущего угла с проставленной точкой: в результате вы получите искомый угол. .
Измерение углов. Транспортир. Виды углов
Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом, записывают так 1 ° .
Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Пример:
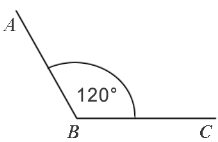
Градусная мера угла ABC равна 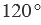 . Говорят: «Угол ABC равен 120 градусам». Пишут:
. Говорят: «Угол ABC равен 120 градусам». Пишут: 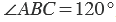 .
.
Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до 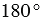 .
.
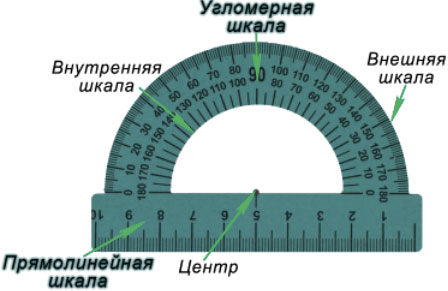
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).
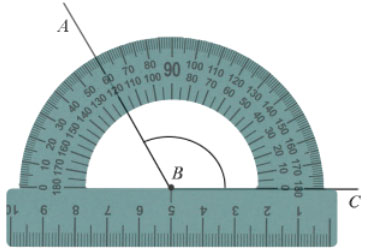
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: 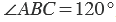 .
.
Свойства:
- Равные углы имеют равные градусные меры.
- Меньший угол имеетменьшую градусную меру.
- Развернутый угол равен
 .
. - Неразвернутый угол меньше
 .
. - Если лучделит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже
 АОС =
АОС =  АОВ +
АОВ +  ВОС.
ВОС.
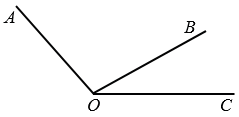
Виды углов:
- Острый угол — угол, градусная мера которого меньше 90 ° .
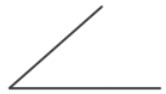
- Прямой угол — угол, градусная мера которого равна 90 ° .

- Тупой угол — угол, градусная мера которого больше 90 °, но меньше 180 ° .
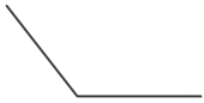
- Развернутый угол — угол, градусная мера которого равна 180 °.
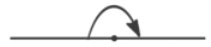
Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90 0 .
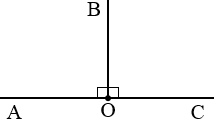
 АОС — развернутый, ОВ — биссектриса,
АОС — развернутый, ОВ — биссектриса,  АОВ =
АОВ =  ВОС = 90 0 .
ВОС = 90 0 .
Поделись с друзьями в социальных сетях:
Что такое транспортир? Правила измерения углов
Что такое транспортир?
Транспортиром называют предмет, с помощью которого каждый из нас может не только измерять углы, но и строить их. Внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части — полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов.

Самодельный угломер из транспортира своими руками
Смотрим видео, как сделать угломер своими руками
[media=https://www.youtube.com/watch?v=uJMauut81hI]
Существуют такие моменты, когда нужно измерить угол какой либо поверхности. На помощь может прийти множество приборов, таких как, например, транспортир, монтажный (или строительный) уровень, угольник и т.д. Но, иногда бывает, что под рукой не оказывается нужных приборов, а нужно точно измерить угол той или иной поверхности. Проанализировав эту проблему, я пришёл к выводу, что можно сделать своими руками в домашних условиях и из домашних приспособлений самодельный прибор, который поможет вам измерить угол любой поверхности, причём, с точностью до 0,5 градуса.
Для угломера нам понадобится следующее: — ненужная рамка для фотографий; — небольшой кусочек картона (по размеру идентичный с размером рамки); — обыкновенный школьный транспортир; — нитка, шайба, двусторонний скотч.
Итак, сначала приготовим транспортир. Для этого привязываем к нему ниточку, на конце которой аккуратно привязываем шайбочку так, как это показано на фотографии. Теперь по краям транспортира наклеиваем двусторонний скотч (это очень важно, так как ниточка должна свободно перемещаться). Теперь прикладываем транспортир так, чтобы ось самого транспортира совпадала с осью рамки для фотографий. Делаем так, как показано на фотографии ниже: Далее убираем рамку и аккуратно приклеиваем скотчем транспортир к картону.
У нас получается вот такая вот конструкция:
Теперь устанавливаем назад (в рамку) стекло (соблюдайте технику безопасности, чтобы избежать ранений).
Далее нужно аккуратно установить заготовку (транспортир с шайбочкой, прикреплённый двусторонним скотчем на картонку) в рамку так, как это показано на фотографии.
Далее нужно всё тщательно проверить, что мы и делаем. Как видим, ниточка с шайбочкой перемещается свободно и прибор работает.
Теперь нужно с помощью кнопок закрепить картонку и рамку.
Ну вот собственно и всё! Прибор для измерения углов (а точнее наклона поверхности) готов. Теперь я покажу как этим угломеров правильно пользоваться. Допустим, мы имеем какую-нибудь наклонную плоскость и нам нужно измерить угол наклона этой поверхности. Мы берём наш прибор и ставим его на поверхность, угол которой нужно измерить. Смотрим на транспортир: ниточка под утяжелением шайбочки и благодаря наклону измеряемой нами поверхности отклоняется на некий градус. Далее по правилам арифметики от показателя градусов ниточкой нужно вычесть 90 градусов и мы получим точный наклон измеряемой нами поверхности в градусах.
Становитесь автором сайта, публикуйте собственные статьи, описания самоделок с оплатой за текст. Подробнее здесь.
Правила пользования
В школе объясняют, что такое транспортир, на уроках математики. Именно здесь есть необходимость в измерениях.
Для того чтобы нам узнать, чему равен один градус, нужно окружность поделить на 360 равных частей. Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.
Нарисуем две окружности разного диаметра и поделим каждую на 360 равных частей. Затем наложим меньшую окружность на большую и увидим, что линии совпали.
Измеряем угол
Транспортир помогает построить и измерить угол. Градус — это общепринятая единица, которой пользуются для измерения углов. Встречается несколько разновидностей углов:
- Острый. Таким называют угол до 90 градусов.
- Прямым является угол, равный 90 градусам.
- Тупой угол варьируется в диапазоне от 90 до 180 градусов.
- Развёрнутый угол представляет собой прямую линию или 180 градусов.
- Полный угол выглядит как окружность и составляет 360 градусов.

Нетрудно разобраться, как измерить угол. Для того чтобы узнать, какова величина угла, нам необходимо установить транспортир таким образом, чтобы его центр располагался в вершине угла, а прямая сторона совпала с одной из его сторон. Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.
Для построения угла с заданным градусом следует приложить прямую часть транспортира к линии, а его центр — к началу линии. Впоследствии эта точка будет являться вершиной угла. Затем на шкале отыскиваем заданное число и ставим точку. Теперь транспортир можно снять и соединить отрезком начало линии (вершину угла) с отмеченной точкой.
Школьные канцтовары, произведенные разными компаниями, отличаются по материалу, цвету, размеру. Так вот: тем, у кого транспортир оказался больше длины угла, и не представляется возможным определить его величину, сторону угла необходимо продлить, используя прямую линейку.
Измерение углов. Транспортир
На этом уроке мы познакомимся с прибором для измерения углов – транспортиром. Научимся с помощью транспортира измерять и строить углы.
Коснёмся истории, чтобы узнать, как появился транспортир
Понятие «градуса» и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне. Хотя само слово градус
имеет латинское происхождение (
градус
– от лат.
gradus
– “шаг, ступень”). Предполагают, что создание транспортира было связано с созданием первого календаря.
Древние вавилонские математики и астрономы полный оборот (окружность) разделили на столько частей, сколько дней в году. Они думали, что в году 360 дней. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень удобным. На нём можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус
. Каждый
градус
разделили на 60
минут
, а
минуту
– на 60
секунд
. Градусная мера сохранилась и до наших дней.
Итак, для измерения углов применяют транспортир
Транспортир
состоит из
линейки
(прямолинейной шкалы) и
полуокружности
(угломерной шкалы).
Центр
этой полуокружности отмечен на транспортире или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.
Если из центра этой полуокружности провести лучи через каждый штрих, то получится 180 углов. Каждый, из которых равен доле развернутого угла.
Определение
Такие углы принято называть градусами

Градусы обозначают вот таким знаком °.
Каждое деление шкалы транспортира равно 1°. Кроме делений по 1° на шкале транспортира есть ещё деления по 5° и по 10°.
А теперь давайте разберёмся, как с помощью транспортира измерить угол. Запомните алгоритм измерения углов
1) Совместить вершину угла с центром транспортира
2) Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчёта на шкале транспортира; 0 – начало отсчёта
3) Найдём штрих на шкале, через который пройдёт вторая сторона угла;
(заметьте, используем ту шкалу для определения градусной меры угла, где располагается нулевой градус)
.
4) Смотрим, через какой штрих проходит вторая сторона и какой градус соответствует этому штриху

На нашем слайде угол АОВ равен 50°. Пишут так:
Развёрнутый угол равен 180°. Так как мы с вами выяснили, что прямой угол равен половине развёрнутого угла, то он равен
Прямой угол
Так как равные углы полностью совмещаются при наложении, то равные углы имеют равные градусные меры
. Следовательно,
больший угол
имеет большую градусную меру,
меньший угол
имеет меньшую градусную меру.

Транспортир применяют и не только для измерения углов, а также и для их построения.
Запомним алгоритм построения углов
Алгоритм будем исследовать на конкретном примере
: построить угол МКN равный 110°.
1. Отметим произвольную точку и обозначим её буквой К
2. Начертим луч с началом в точке А и на нём отметим произвольную точку М. Получили луч КМ
3. Наложим транспортир так, чтобы центр его совпал с точкой К, а луч КМ прошёл через начало отсчёта на шкале
4. На этой же шкале транспортира найдём штрих, который соответствует 110°. Отметим на чертеже точку
Nпротив штриха с отметкой 110°
.
5. Проведём луч КN. Построенный нами угол МКN
иесть искомый
.
6. Не забудем записать МКN
= 110°
.
Такой же угол можно построить и по другую сторону от луча КМ.
Повсюду есть углы любые: Прямые, острые, тупые, Есть смежные, развёрнутые есть, Их много, всех не перечесть.
Определение
Если угол меньше 90°, то его называют острым углом
Если угол больше 90°, но меньше 180°, то его называют тупым углом
На экране изображены угол АОС – острый
и угол МКN –
тупой
. Градусная мера угла АОС равна 30°, т.е. меньше 90°, следовательно, он
острый
. Градусная мера угла МКN равна 120°, т.е. больше 90°, но меньше 180°, следовательно, он
тупой
.
Итак, сегодня на уроке мы познакомились с прибором для измерения углов – транспортиром. Научились с помощью него измерять и строить углы.
Набор школьника
Неспроста учащиеся младшего звена не знакомы с транспортиром. При его применении должна быть заложена некая база знаний. Для полноценной работы с ним на уроке ребята изучают ряд сопутствующих предметов. Прежде чем узнать, что такое транспортир, школьники должны в совершенстве овладеть прямой линейкой, чертить ровные линии, изучить сложение и вычитание, освоить циркуль, знать геометрические фигуры и так далее. Весь этот процесс занимает время, и только окончив начальную школу, ученик может добавить транспортир в свой набор инструментов.

Ученикам сейчас предлагаются школьные канцтовары в огромном выборе. Транспортир не исключение. Производители стараются угодить самым требовательным запросам покупателей. Инструменты изготавливают в различной цветовой гамме. Яркие цвета всегда нравятся детям. Порой даже в одном классе не сыскать одинаковых транспортиров, что облегчает при утрате их поиск. Формы и размеры каждый выбирает на свой вкус.
Большинство таких товаров выпускают из пластмассы, и это значительно уменьшает его стоимость. Но есть деревянные и даже железные транспортиры. Как показывает практика, металлические хоть и непрозрачны, но практичнее в том плане, что шкала не стирается, а это позволяет гораздо дольше применять его в действии, с точностью определяя углы.
Транспортир не так востребован школьниками, как линейка, но он сопровождает учеников вплоть до выпускного экзамена. Некоторые из выпускников школы выбирают специальности, которые связаны с измерением и построением углов, проектированием зданий и сооружений, работой с чертежами. В силу своих профессий им постоянно приходится сталкиваться с транспортирами и его производными. Но и бывшие одноклассники нынешних инженеров, порой даже с глубочайшим гуманитарным уклоном, без труда вспомнят навыки обращения с этим предметом и определят количество градусов у любого угла.
Урок математики по теме «Измерение углов. Транспортир». 5-й класс
Класс: 5
Презентация к уроку
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели:
- Образовательные:
- познакомить учащихся с единицей измерения углов, с прибором для измерения углов;
- научить пользоваться транспортиром.
- Развивающие:
- развивать внимание, мышление учащихся;
- развивать самостоятельность учащихся, используя проблемные ситуации, творческие задания;
- развивать познавательный интерес к предмету.
- Воспитательные:
- воспитывать чувство взаимоуважения;
- воспитывать у учащихся навыки учебного труда.
I. Организационный момент
II. Вступительное слово учителя
Мы познакомимся с измерительным прибором (как он называется, вы узнаете немного позже), научимся с его помощью измерять, а затем и строить углы. Вы покажите свои знания, докажите насколько внимательны.
Будем учиться не только математике, но и умению общаться, уважению друг к другу.
Для того чтобы достичь наших целей, вы должны быть волевыми, настойчивыми, целеустремленными, поэтому эпиграфом нашего урока будут слова:
| «Усердие все превозмогает» |
III. Устная работа
Какие из углов, изображенных на рисунке, являются:
а) острыми;
б) тупыми;
в) есть ли среди этих углов прямые?

О каком угле мы с вами еще не вспомнили? [О развернутом]
Какой угол называется развернутым? Острым? Прямым? Тупым?
Мы знаем, что два угла можно сравнивать друг с другом.
Какой способ для этого мы использовали? [Наложение]
Но углы, также как и отрезки, можно сравнивать не только наложением, но и с помощью измерения.
IV. Изучение нового материала
Для построения и измерения углов используют специальный прибор. Как он называется, вы узнаете, отгадав кроссворд.

1. Результат деления.
2. Лучи образующие угол.
3. Точка, из которой выходят лучи образующие угол.
4. Угол, который образуют два дополнительных друг другу луча.
5. Результат сложения.
6. Угол, который составляет половину развернутого угла.
7. Инструмент, который используют для построения прямого угла.
8. Угол, меньше прямого.
9. Угол, больше прямого, но меньше развернутого.
10. Результат умножения.
11. Результат вычитания.
Учитель демонстрирует учащимся транспортир или показывает на плакате:
– Для измерения углов применяют транспортир. Положите перед собой транспортиры. Вы видите, какие они разные, но у всех есть нечто общее, о чем мы сейчас будем говорить.
Слайд 5. Итак, шкала транспортира. Она расположена на полуокружности и пронумерована
от 0 до 180. Бывают шкалы двойные: нумерация идет слева направо и справа налево.

Слайд 6. Также есть круглые транспортиры, шкала идет по кругу от 0 до 360, но она также разделена на две полуокружности.

Центр этой полуокружности отмечен на транспортире точкой или черточкой. Найдите на своем транспортире центр и покажите его.
Штрихи шкалы транспортира делят полуокружность на 180 равных частей. Лучи, проведенные из центра полуокружности через эти штрихи, образуют 180 углов, каждый из которых равен  доле развернутого угла. Такие углы называют градусами.
доле развернутого угла. Такие углы называют градусами.
Слайд 7. Итак, градусом называют  долю развернутого угла. Градусы обозначают знаком °. Каждое деление шкалы транспортира равно 1°.
долю развернутого угла. Градусы обозначают знаком °. Каждое деление шкалы транспортира равно 1°.
Историческая справка
Слово «градус» – латинское, означает «шаг», «ступень». Измерение углов в градусах появилось более 3 тыс. лет назад в Вавилоне. В расчетах там использовались шестидесятеричная система счисления, шестидесятеричные дроби.
С этим связано, что вавилонские математики и астрономы, а вслед за ними греческие и индийские, полный оборот (окружность) делили на 360 частей – градусов (шесть раз по шестьдесят), каждый градус – на 60 минут, а минуту – на 60 секунд:

Объяснение учителя (с демонстрацией на доске), как с помощью транспортира можно измерить угол.
– Как измеряют углы с помощью транспортира?
1) Нужно вершину угла совместить с центром транспортира.
2) Одна сторона угла должна проходить через нулевую отметку (0° по шкале).
3) Вторая сторона угла должна пересекать шкалу. Нужно посмотреть, через какую
отметку проходит вторая сторона угла. Это и есть величина этого угла.
Если у транспортира есть две шкалы, то надо смотреть на отметку той шкалы, через ноль которой проходит одна из сторон угла.
V. Практическая работа
Каждому ученику выдается набор углов: острый, прямой, тупой и развернутый.

Задания
- Выберите из предложенных вам углов острый, тупой, прямой, развернутый.
- Измерьте их градусную меру и запишите в тетрадях эти данные.
- Сделайте вывод о градусной мере:
а) развернутого угла;
б) прямого угла;
в) острого угла;
г) тупого угла.
Вывод:
| – развернутый угол равен 180°; – прямой угол равен 90° (половина развернутого угла); – острый угол меньше 90°; – тупой угол больше 90°, но меньше 180°. |
VI. Физкультурная пауза
- Покажите руками угол 90°, 180°.
- Покажите руками острый угол, тупой угол.
- Покажите рукой, где вокруг нас есть прямые углы.
- Повернитесь на 180°. А теперь на 90°.
Задание: Начертите в тетради угол любой величины. Предложите соседу по парте его измерить.
VII. Работа по карточкам
У всех учеников карточки с одинаковым заданием.
Задание: Измерьте углы и запишите результаты измерений в тетрадях.

Задание: Выполняется устно с использованием модели часов.
Какой угол образуют часовая и минутная стрелки часов:
а) в 3 ч; в) в 10 ч; д) в 2 ч 30 мин;
б) в 5 ч; г) в 6 ч; е) в 5 ч 30 мин?
Задача №1652
Луч ОС лежит внутри угла АОВ, причем  АОС = 37°,
АОС = 37°,  ВОС = 19°?.
ВОС = 19°?.
Активный туризм на Юге России
1.15. ИЗМЕРЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ ПО КАРТЕ
Измерение транспортиром. Тонко очиненным карандашом, аккуратно по линейке, прочерчивают линию через главные точки условных знаков исходного пункта и ориентира. Длина прочерченной линии должна быть больше радиуса транспортира, считая от точки ее пересечения с вертикальной линией координатной сетки. Затем совмещают центр транспортира с точкой пересечения и поворачивают его, сообразуясь с величиной угла, как показано на рис. 27. Отсчет против прочерченной линии при положении транспортира, указанном на рис. 27, а, будет соответствовать величине дирекционного угла, а при положении транспортира, указанном на рис. 27,6, к полученному отсчету необходимо прибавить 180°.
При измерении дирекционного угла необходимо помнить, что дирекционный угол отсчитывается от северного направления вертикальной линии сетки по ходу часовой стрелки.
Средняя ошибка измерения дирекционного угла транспортиром, имеющимся на командирской линейке, примерно равна 1°. Большим транспортиром (с радиусом 8—10 см) угол на карте можно измерить со средней ошибкой 15′.
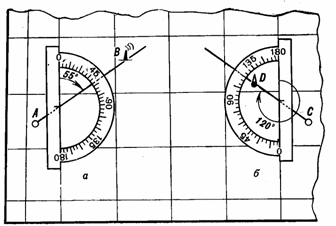
Рис. 27. Измерение дирекционных углов транспортиром
Измерение хордоугломером (рис. 28). Через главные точки условных знаков исходного пункта и ориентира проводят на карте тонкую прямую линию длиной не менее 12 см. Из точки пересечения этой линии с вертикальной линией сетки карты циркулем делают на них засечки радиусом, равным расстоянию на хордоугло-мере от 0 до 10 больших делений. Засечки делают на линиях, образующих острый угол.
Затем измеряют хорду — расстояние между отметками отложенных радиусов. Для этого левую иглу циркуля-измерителя с отложенной хордой передвигают по крайней левой вертикальной линии шкалы хордоугломера до тех пор, пока правая игла циркуля не совпадет с каким-либо пересечением наклонной и горизонтальной линии. При этом правую иглу необходимо передвигать строго на одном уровне с левой. В таком положении циркуля производят отсчет против его правой иглы. По верхней части шкалы отсчитывают большие и десятки малых делений. По левой части шкалы с ценой делений 0-01 уточняют величину угла. Пример измерения угла хордоугломером показан на рисунке.
С помощью хордоугломера измеряют острый угол от ближайшей вертикальной линии координатной сетки, а дирекционный угол отсчитывают от северного направления линии сетки по ходу часовой стрелки. Значение дирекционного угла определяют по изме-
Рис. 28. Измерение дирекционого угла хордоугломером
ренному углу в зависимости от четверти, в которой расположен ориентир. Зависимость между измеренным углом а’ и дирекционным углом а показана на рис. 29.
Углы хордоугломером можно измерить си средней ошибкой 0-01—0-02 дел. угл. (4— 8′).
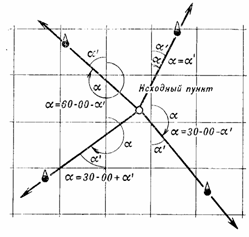
Рис. 29. Переход от угла а’, измеренного хордоугломером, к дирекционному углу а
Измерение артиллерийским кругом. Центр круга совмещают с исходным пунктом (главной точкой условного знака) и круг устанавливают так, чтобы диаметр его 0—30 был параллелен вертикальным линиям координатной сетки, а нуль направлен на север. Затем масштабную линейку совмещают с главной точкой условного знака ориентира и на пересечении ребра линейки со шкалой круга считывают величину угла.
Артиллерийским кругом можно измерить дирекционный угол и без масштабной линейки (рис. 30). В этом случае предварительно прочерчивают на карте линию через главные точки условных знаков исходного пункта и ориентира. Затем артиллерийский круг устанавливают, как указано выше, и против прочерченной линии считывают по шкале круга величину дирекционного угла.
Рис. 30. Измерение дирекционного угла артиллерийским кругом
Артиллерийским кругом дирекционный угол. можно измерить со средней ошибкой 0-03 дел. угл.
Измерение углов. Транспортир
Урок 43. Математика 5 класс

Конспект урока «Измерение углов. Транспортир»
На этом уроке мы познакомимся с прибором для измерения углов – транспортиром. Научимся с помощью транспортира измерять и строить углы.
Коснёмся истории, чтобы узнать, как появился транспортир.
Понятие «градуса» и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне. Хотя само слово градус имеет латинское происхождение (градус – от лат. gradus – “шаг, ступень”). Предполагают, что создание транспортира было связано с созданием первого календаря.
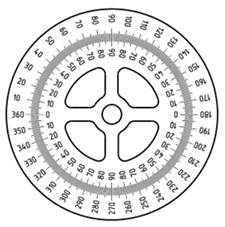
Древние вавилонские математики и астрономы полный оборот (окружность) разделили на столько частей, сколько дней в году. Они думали, что в году 360 дней. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень удобным. На нём можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Каждый градус разделили на 60 минут, а минуту – на 60 секунд. Градусная мера сохранилась и до наших дней.
Итак, для измерения углов применяют транспортир.

Транспортир состоит из линейки (прямолинейной шкалы) и полуокружности (угломерной шкалы). Центр этой полуокружности отмечен на транспортире или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.
Если из центра этой полуокружности провести лучи через каждый штрих, то получится 180 углов. Каждый, из которых равен 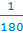 доле развернутого угла.
доле развернутого угла.
Определение
Такие углы принято называть градусами.
Градусы обозначают вот таким знаком °.
Каждое деление шкалы транспортира равно 1°. Кроме делений по 1° на шкале транспортира есть ещё деления по 5° и по 10°.
А теперь давайте разберёмся, как с помощью транспортира измерить угол. Запомните алгоритм измерения углов:
1) Совместить вершину угла с центром транспортира.
2) Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчёта на шкале транспортира; 0 – начало отсчёта.
3) Найдём штрих на шкале, через который пройдёт вторая сторона угла; (заметьте, используем ту шкалу для определения градусной меры угла, где располагается нулевой градус).
4) Смотрим, через какой штрих проходит вторая сторона и какой градус соответствует этому штриху.
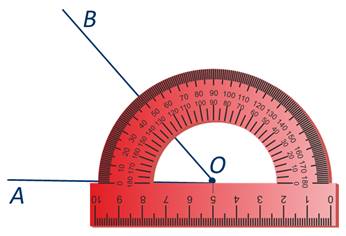
На нашем слайде угол АОВ равен 50°. Пишут так:
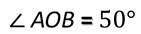
Развёрнутый угол равен 180°. Так как мы с вами выяснили, что прямой угол равен половине развёрнутого угла, то он равен
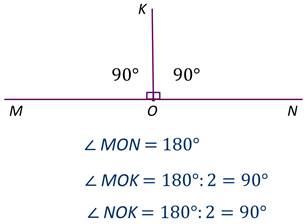
Прямой угол равен 90°.
Так как равные углы полностью совмещаются при наложении, то равные углы имеют равные градусные меры. Следовательно, больший угол имеет большую градусную меру, меньший угол имеет меньшую градусную меру.
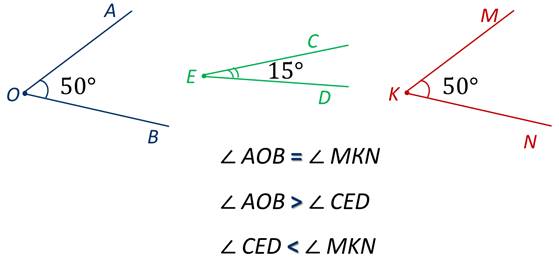
Транспортир применяют и не только для измерения углов, а также и для их построения.
Запомним алгоритм построения углов.
Алгоритм будем исследовать на конкретном примере: построить угол МКN равный 110°.
1. Отметим произвольную точку и обозначим её буквой К.
2. Начертим луч с началом в точке А и на нём отметим произвольную точку М. Получили луч КМ.

3. Наложим транспортир так, чтобы центр его совпал с точкой К, а луч КМ прошёл через начало отсчёта на шкале.
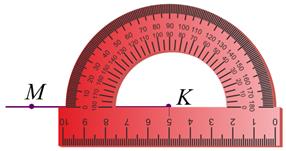
4. На этой же шкале транспортира найдём штрих, который соответствует 110°. Отметим на чертеже точку N против штриха с отметкой 110°.
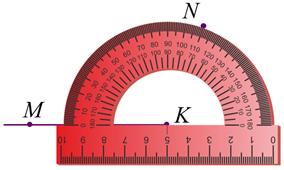
5. Проведём луч КN. Построенный нами угол МКN и есть искомый.
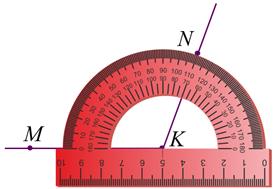
6. Не забудем записать МКN = 110°.
МКN = 110°.
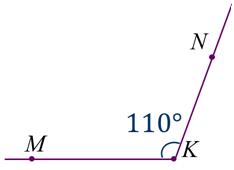
Такой же угол можно построить и по другую сторону от луча КМ.
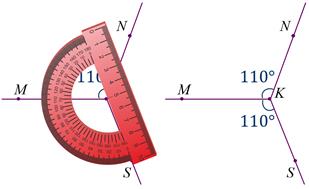
Повсюду есть углы любые:
Прямые, острые, тупые,
Есть смежные, развёрнутые есть,
Их много, всех не перечесть.
Определение
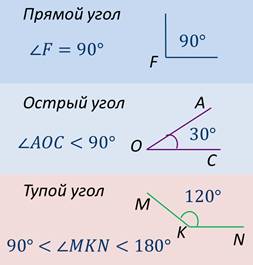
Если угол меньше 90°, то его называют острым углом.
Если угол больше 90°, но меньше 180°, то его называют тупым углом.
На экране изображены угол АОС – острый и угол МКN – тупой. Градусная мера угла АОС равна 30°, т.е. меньше 90°, следовательно, он острый. Градусная мера угла МКN равна 120°, т.е. больше 90°, но меньше 180°, следовательно, он тупой.
Итак, сегодня на уроке мы познакомились с прибором для измерения углов – транспортиром. Научились с помощью него измерять и строить углы.
Как пользоваться рулеткой. Фишки, о которых мало кто знает


В Соединенных Штатах есть праздник — национальный День строительной рулетки. Что ж, мы тоже знаем, как выглядит рулетка. Большинству из нас хотя бы раз приходилось ею пользоваться на работе или дома, чтобы узнать длину, высоту или ширину какого-то предмета. Но этот, вроде бы, незамысловатый инструмент — не так прост, как может показаться.
На самом деле у рулеток есть целый ряд неочевидных особенностей, которые позволяют мастеру существенно расширить измерительные возможности, благодаря которым измерения становятся проще и точнее.
За более чем 150-летнюю историю рулетка перестала быть просто гибким аналогом линейки. С момента появления (первый образец с металлическим скручивающимся полотном представил британец Джеймс Честерман в 1865 году) она прошла путь до недешевых высокотехнологичных девайсов с электронными модулями и дисплеями. В них интегрированы лазеры, пузырьковые уровни, режущие элементы, разметочные приспособления. Но сейчас речь пойдет о самых обычных рулетках.

Подвижный зацеп
Большинство пользователей, взяв в руки новую рулетку, обращают внимание на довольно сильный люфт металлического зацепа, закрепленного на конце полотна, и на странные прорези в металле возле заклепок.

Некоторые мастера считают своим долгом исправить ситуацию, поэтому собственноручно фиксируют зацеп, добивая заклепки до полного сжатия.
На самом деле такая подвижность — это не баг, а фича. Дело в том, что рулеткой измеряют либо цепляя ее, либо прислоняя. Сам зацеп сделан из изогнутой пластины имеющей собственную толщину (около 1 мм), которую необходимо как-то компенсировать, чтобы получить точные результаты. Вот для такой компенсации этот «ограниченный» люфт как раз и служит.

Зацеп имеет сложную двухстороннюю форму
Измерять или производить разметку иногда приходится в неудобном положении, в стесненных условиях на неровных предметах. Чтобы добиться стабильности и хорошей читаемости полотна — некоторые производители ушли от простой L-образной формы зацепа. В итоге получился более практичный элемент с ножками или с одним лепестком.

Иногда очень удобно, когда зацеп шире полотна — можно легко увидеть деления, находясь сбоку.

Один известный инструментальный производитель пошел немного дальше, выпустив рулетку со съемными зацепами разной формы.
Острый край зацепа
Иногда зацеп строительной рулетки имеет зазубрины на краю или своеобразное острие. Такое решение позволяет на мягких материалах (например, на плите гипсокартона или на шпаклевке) делать разметку самой рулеткой без использования карандаша — прочерчивая на поверхности линии металлической кромкой.
Удобнее, если кроме заостренного зацепа на корпусе тоже есть специальный металлический зуб. Используя эти «якоря», можно действовать «царапающим шаблоном».

Вырез в зацепе используют для того, чтобы можно было поставить в искомой точке метку карандашом.

Магнитные вставки
Для тех, кто часто работает со стальными деталями, магнитящий зацеп стал настоящей находкой. С его помощью можно легко зафиксировать полотно рулетки встык с металлическим профилем или, например, подвесить рулетку в растянутом состоянии от потолка.

Данная опция реализована по-разному. Одни производители устанавливают маленькие неодимовые магниты в отверстия зацепа, другие сделали отдельный съемный узел. Очень полезным оказалось решение, когда один из магнитов располагается непосредственно под полотном, что дает возможность без проблем измерять такие неудобные материалы как трубы.

Хорошие магнитные рулетки способны выдерживать собственный вес, а некоторые из них запросто удерживают на магните такие тяжелые предметы как молоток.
В случае необходимости полотном рулетки с магнитом на конце можно доставать мелкие металлические детали и крепежи, упавшие в какое-нибудь труднодоступное место.
Отверстие в зацепе
В металлической пластине L-образного зацепа часто можно обнаружить удлиненное отверстие. Необходимо оно, чтобы можно было зафиксировать край рулетки за головку отдельно стоящего крепежа. Кроме всего прочего эту особенность можно использовать, чтобы очертить окружность — просто нужно сначала в ее центр вкрутить саморез, а потом, двигая рулетку по кругу, обрисовать необходимый контур.

Приспособления для разметки круга
Речь идет о возможности зафиксировать рулетку в одной точке (которая будет центром круга) на относительно мягкой поверхности. Есть несколько вариантов решений этого вопроса:
- Выдвижной острый зуб на корпусе строительной рулетки.
- Заклепка со сквозным отверстием, расположенная где-то на краю полотна. Через это отверстие в поверхность втыкают шило, что позволяет очертить круг (еще это поможет без посторонней помощи просто растянуть хорошо закрепленное полотно на большое расстояние).

Возможность точного измерения во внутренних углах
Измеряя расстояние между противоположными стенами в комнате, достаточно сложно получить точные данные из-за невозможности полностью перегнуть полотно рулетки в углу. Разумеется, такой проблемы нет, если вы пользуетесь лазерным дальномером, однако тут приходится смириться с некоторой погрешностью.

Но выход, как оказалось, есть. Достаточно просто знать размеры корпуса рулетки и поставить ее впритык со стеной. А потом нужно всего лишь прибавить к полученному результату эту цифру. Кстати, некоторые производители именно для этого указывают на рулетке ширину ее корпуса.


Измерение окружности предмета
Чтобы измерить или скопировать округлый предмет, нужно обмотать его полотном рулетки. А чтобы считывать результаты было легче — на тыльной стороне полотна нанесена специальная разметка с отдельно вынесенным нулем.

Вообще наличие разметки на тыльной стороне сейчас считается правилом хорошего тона у известных зарубежных производителей. Зачастую тут можно наблюдать вертикальное расположение цифр — для более удобного измерения высоты.
Широкое изогнутое полотно
Чтобы выполнить замеры при помощи рулетки, строителям, работающим без помощника, часто приходится растягивать полотно на весу. Чтобы полотно хорошо держало свою форму и не перегибалось под собственным весом — его делают увеличенной ширины и с заметным продольным изгибом. Хорошие самонесущие способности рулеточного полотна являются несомненным плюсом.
Расстояние, до которого полотно можно свободно выпустить из корпуса на весу, иногда дополнительно обозначается на шкале.

Вспомогательные риски на разметке
В некоторых рулетках на тыльной и лицевой стороне полотна, производители нанесли точки или какие-то другие специальные значки. Это циклично расставленные согласно общепринятым стандартам (в среднем около 30, 40, 60 сантиметров) отметки, по которым мастера быстро монтируют несущие элементы различных строительных каркасов. Например, кровельные стропила или балки перекрытия.

Римские цифры на рабочей шкале
На лицевой стороне полотна рулетки (недалеко от края) могут наносить знак сертификации СЕ, здесь же указывают класс точности, который обозначается римскими цифрами. Показатель класса точности отображает погрешности, которые набегают в процессе разметки рулеточного полотна при производстве.

Как видим, современные строительные рулетки в умелых руках способны на многое. Они практичны и информативны, точны и долговечны. Однако, выбирая измерительный инструмент, не стоит экономить без оглядки, ведь, как показывает практика, по-настоящему качественная рулетка доставит истинное удовольствие от работы и точно оправдает потраченные средства.



